Ohm’s law cannot be applied to solve complex circuits where series and parallel simplification are impossible. Kirchhoff’s gave two laws to solve such complex circuits; they are,

(i) Kirchhoff’s Current Law (KCL)

(ii) Kirchhoff’s Voltage Law (KVL)

(I) Kirchhoff’s Current Law :

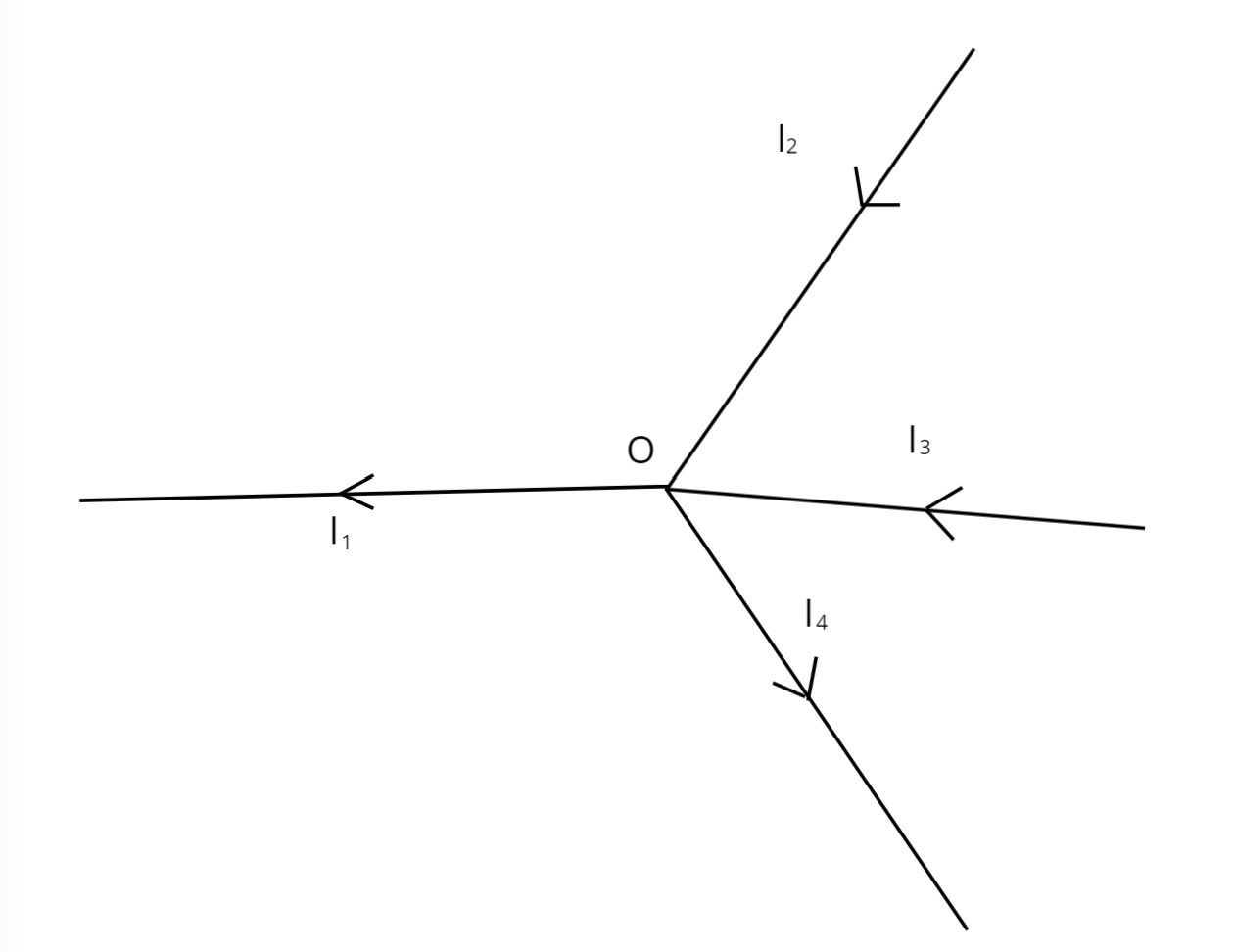
Kirchhoff’s Current Law states that “the algebraic sum of the currents entering into the junction is equal to the leaving from the junction.. Hence the accumulation of charges at the junction is zero.”.

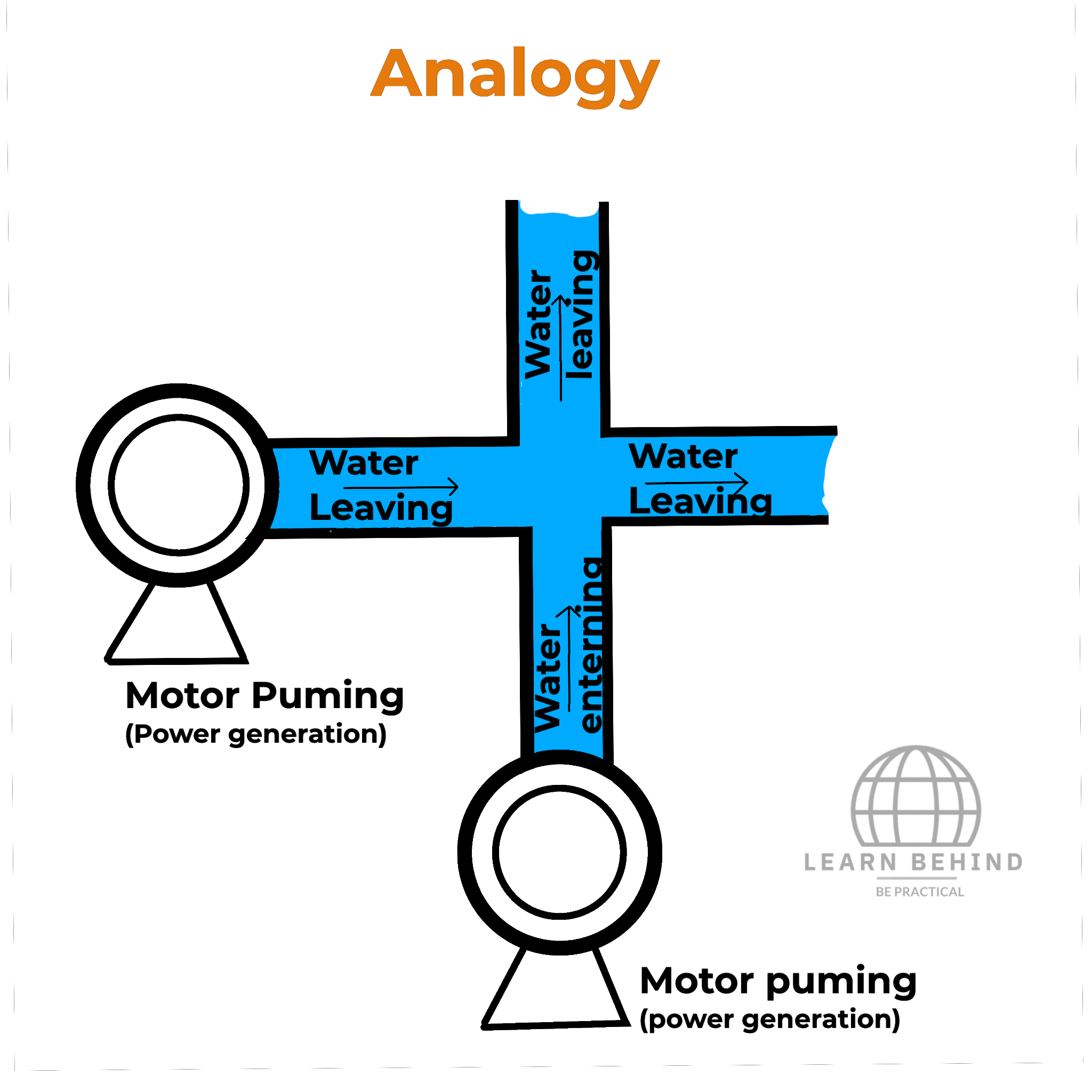
Imagine a tank with a motor pump circulating water through a pipe. Consider the pipe as a conductor and water as current. When the motor starts pumping, the water entering the pipe must equal the water leaving the pipe, and there's no accumulation of water at any junction. This principle is analogous to Kirchhoff's Current Law.

Let us assume four conductors are carrying current I₁, I₂ ,I₃, and I₄ connecting at the 0 as shown in figure. From the figure, if you take entering current as positive and leaving as current as negative .Then, applying Kirchhoff’s current law to the junction 0 , we have,

(I₁) + (I₂) + (-I₃) + (-I₄) = 0

I₁ + I₂ = I₃ + I₄

Sum of entering currents = sum of outgoing currents

(II) Kirchhoff’s Voltage law:

The Kirchhoff’s Voltage law is define as “The algebraic sum of all voltages around any closed loop in circuit is equal to zero.”

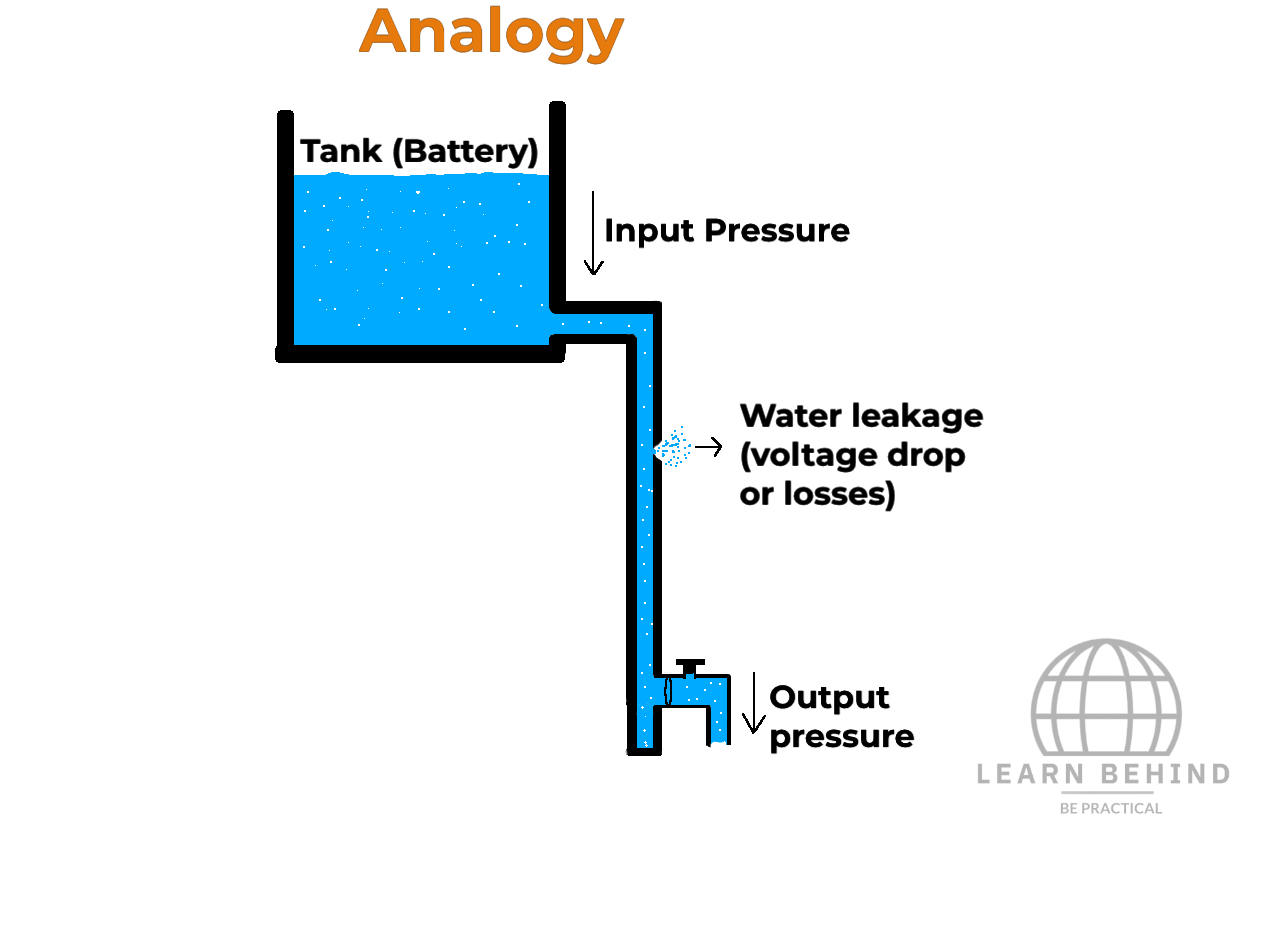
Imagine a tank as a cell, water pressure as voltage, and a pipe as a conductor. In a water circulation system, the input water pressure must equal the output pressure of the pipe, and there is no pressure accumulation. This principle is analogous to Kirchhoff's Voltage Law.

While applying Kirchhoff’s Voltage Law, it is very important to assign proper signs to emf’s and voltage drops in the closed circuit, and the following sign conventions should be followed:

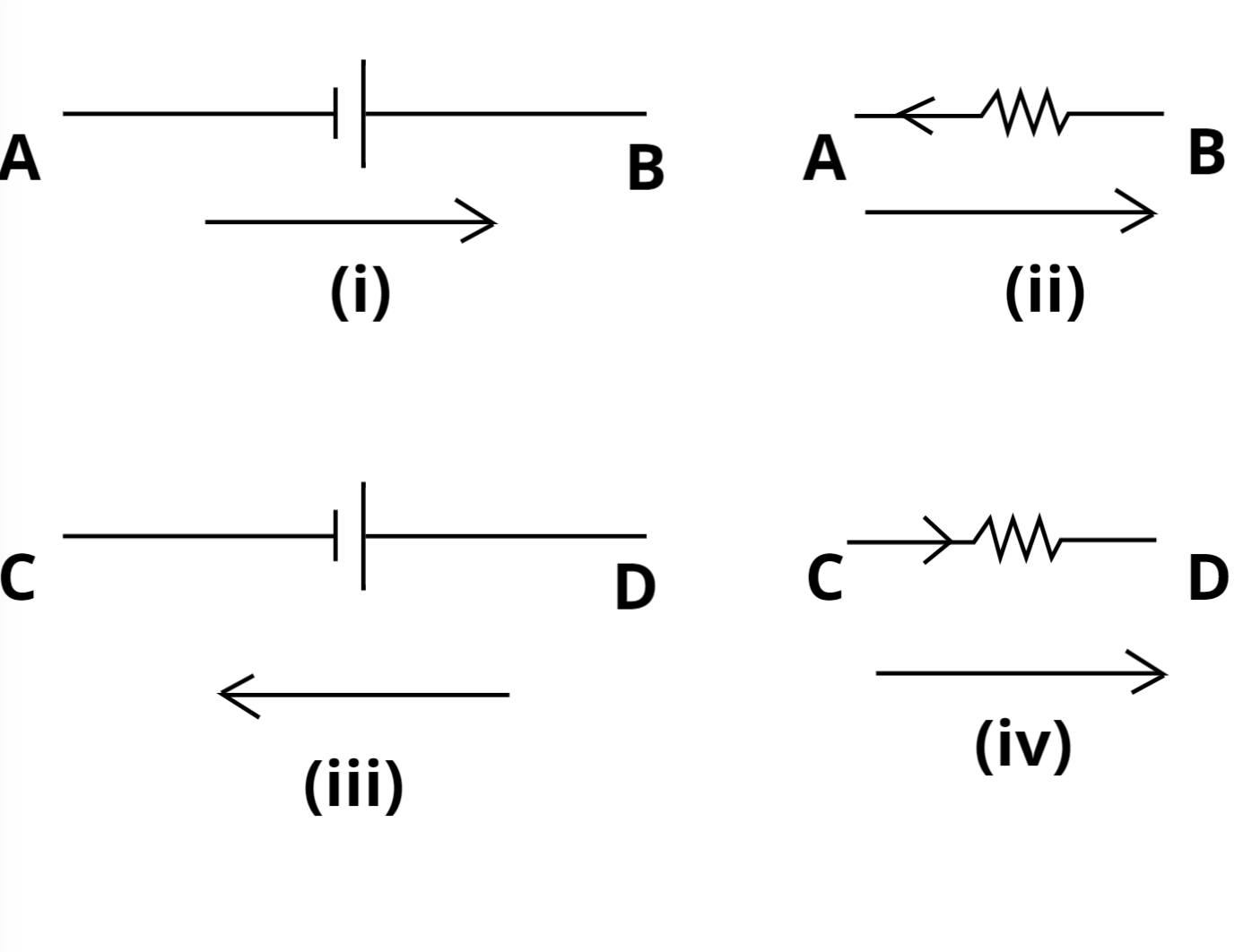
(i) A rise in potential should be treated as positive, and a fall in potential should be considered negative. From the above figure, as we go from A to B (i.e., from the negative terminal to the positive terminal of the cell), There is a rise in potential, and as we go from A to B in figure 2, there is also a rise in potential.

(ii) In figure 3, as we go from C to D, there is a fall in potential, and in figure 4, as we go from C to D, there is again a fall in potential.